ফাংশনঃ SSC Higher Math-Chapter 1.2
ফাংশনঃ অন্বয় ও ফাংশন, অন্বয়ের ডোমেন, অন্বয়ের সদস্য, অন্বয়ের রেঞ্জ, ডোমেন, রেঞ্জ, বিপরীত অন্বয়, অন্বয়ের লেখচিত্র, মান নির্ণয়।
১. {(2,2),(4,2),(2,10),(7,7)} অন্বয়ের ডোমেন কোনটি?
ক) {2,4,5,7} খ) {2,2,10,7}
গ) {2,4,10,7} ঘ) {2,4,7}
উত্তরঃ ক
২. S={(x,y):x∈A, y∈A এবং y=x2} এবং A={-2,-1,0,1,2} নিচের কোনটি S অন্বয়ের সদস্য?
ক) (2,4) খ) (-4,4) গ) (-1,1) ঘ) (1,-1)
উত্তরঃ গ
[y=x2 তে x=-1 বসালে y=(-1)2=1 হবে, অর্থাৎ (x,y)=(-1,1)]
৩. যদি S={(1,4),(2,1),(3,0),(4,1),(5,4)} হয় তবে,
(i) S অন্বয়ের রেঞ্জ {4,1,0}
(ii) S অন্বয়ের বিপরীত অন্বয়, S-1={(4,1),(1,2),(0,3),(1,4),(4,5)}
(iii) S অন্বয়টি একটি ফাংশন
উপরের তথ্যের আলোকে নিচের কোনটি সঠিক?
ক) i. ও ii. খ) ii. ও iii. গ) i. ও iii. ঘ) i, ii. ও iii.
উত্তরঃ খ
৪. যদি F(x)=√(x-1) হয় তবে F(10)=কত?
ক) 9. খ) 3. গ) -3. ঘ) √10.
উত্তরঃ খ
৫. S={(x,y) : x2+y2-25=0 এবং x≥0} হলে,
(i) অন্বয়টি ফাংশন নয়।
(ii) অন্বয়টির লেখচিত্র একটি অর্ধবৃত্ত।
(iii) অন্বয়টির লেখচিত্র x অক্ষের উপর অর্ধতলে থাকবে।
নিচের কোনটি সঠিক?
ক) i. ও ii. খ) ii. ও iii. গ) i. ও iii. ঘ) i, ii. ও iii.
উত্তরঃ ক
৬. F(x)=√(x-1)=5 হলে x এর মান কত?
ক) 5. খ) 24. গ) 25. ঘ) 26.
উত্তরঃ ঘ
৭. F(x)=√(x-1) ফাংশনটির ডোমেন নিচের কোনটি?
ক) ডোম F={x∈R : x≠1} খ) ডোম F={x∈R : x≥1}
গ) ডোম F={x∈R : x≤1} ঘ) ডোম F={x∈R : x>1}
উত্তরঃ খ
৮. (i) নিচে প্রদত্ত S অন্বয়গুলোর ডোমেন, রেঞ্জ ও বিপরীত অন্বয় নির্ণয় কর।
(ii) S অথবা S-1 অন্বয়গুলো ফাংশন কিনা তা নির্ধারণ কর।
(iii) ফাংশনগুলো এক-এক কিনা নির্ধারণ কর।
ক) S={(1,5),(2,10),(3,15),(4,20)}
খ) S={(-3,8),(-2,3),(-1,0),(0,-1),(1,0),(2,3),(3,8)}
গ) S={(½,0),(1,1),(1,-1),(0,0),(5/2,2),(5/2,-2)}
ঘ) S={(-3,-3),(-1,-1),(0,0),(1,1),(3,3)}
ঙ) S={(2,1),(2,2),(2,3)}
সমাধানঃ
(ক)
(i) এখানে, S={(1,5),(2,10),(3,15),(4,20)}
ডোম S={1,2,3,4}
রেঞ্জ S={5,10,15,20}
S-1={(5,1),(10,2),(15,3),(20,4)}
(ii) এখানে S এর একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় নেই। সুতরাং S একটি ফাংশন।
আবার, S-1 অন্বয়েরও একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় নেই। সুতরাং S-1 অন্বয়টিও একটি ফাংশন।
(iii) S={(1,5),(2,10),(3,15),(4,20)}
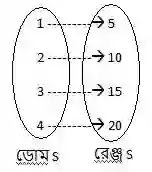
S ফাংশনের ডোমেনের ভিন্ন ভিন্ন সদস্যের প্রতিচ্ছবি ভিন্ন ভিন্ন।
∴S এক-এক ফাংশন।
আবার, S-1={(5,1),(10,2),(15,3),(20,4)}

S-1 ফাংশনের ডোমেনের ভিন্ন ভিন্ন সদস্যের প্রতিচ্ছবি ভিন্ন ভিন্ন।
∴S-1 এক-এক ফাংশন।
(খ)
(i) এখানে, S={(-3,8),(-2,3),(-1,0),(0,-1),(1,0),(2,3),(3,8)}
ডোম S={-3,-2,-1,0,1,2,3}
রেঞ্জ R={-1,0,3,8}
S-1={(8,-3),(3,2),(0,-1),(-1,0),(0,1),(3,2),(8,3)}
(ii) এখানে S এর একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় নেই। সুতরাং S একটি ফাংশন।
আবার, S-1 এর একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় আছে। যেমনঃ (0,-1) এবং (0,1)। সুতরাং S-1 একটি ফাংশন নয়।
(iii) S={(-3,8),(-2,3),(-1,0),(0,-1),(1,0),(2,3),(3,8)}
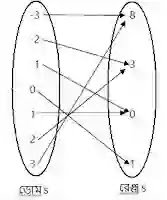
এই ফাংশনের একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় নেই। কিন্তু দ্বিতীয় উপাদান বিশিষ্ট একাধিক ক্রমজোড় আছে। যেমনঃ (-3,8) ও (3,8)। সুতরাং এটি এক-এক ফাংশন নয়।
∴S এক-এক ফাংশন নয়।
আবার,
S-1={(8,-3),(3,2),(0,-1),(-1,0),(0,1),(3,2),(8,3)}
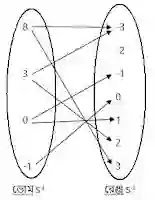
S-1 এ একই প্রথম উপাদান বিশিষ্ট (0,-1) ও (0,1) ক্রমজোড় আছে। কাজেই এটি ফাংশন নয়। সুতরাং এটি এক-এক ফাংশন নয়।
(গ)
(i) S={(½,0),(1,1),(1,-1),(0,0),(5/2,2),(5/2,-2)}
ডোম S={½,1,5/2 }
রেঞ্জ S={-2,-1,0,1,2}
S-1={(0,½), (1,1), (-1,1), (2,5/2),(-2,5/2)}
(ii) S এর একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় আছে, যেমনঃ (1,1) এবং (1,-1)।
∴ S ফাংশন নয়।
S-1 এর একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় নেই।
∴ S-1 একটি ফাংশন।
(iii) S={(½,0),(1,1),(1,-1),(0,0),(5/2,2),(5/2,-2)}
যেহেতু S ফাংশন নয় তাই S এক-এক ফাংশন নয়।
S-1={(0,½), (1,1), (-1,1), (2,5/2),(-2,5/2)}
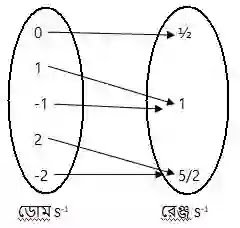
S-1 এর ফাংশনটির একই দ্বিতীয় উপাদান বিশিষ্ট একাধিক ক্রমজোড় আছে, যেমন (1,1) ও (-1,1)। সুতরাং এটি এক-এক ফাংশন নয়।
(ঘ)
(i) S={(-3,-3),(-1,-1),(0,0),(1,1),(3,3)}
ডোম S={-3,-1,0,1,3}
রেঞ্জ S={-3,-1,0,13}
S-1={(-3,-3),(-1,-1),(0,0),(1,1),(3,3)}
(ii) S এর একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় নেই। সুতরাং S একটি ফাংশন।
S-1 এরও একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় নেই। সুতরাং S-1 একটি ফাংশন।
(iii) S={(-3,-3),(-1,-1),(0,0),(1,1),(3,3)}
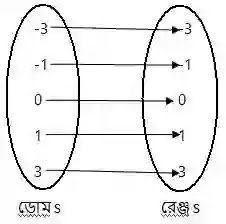
S ফাংশনের ডোমেনের ভিন্ন ভিন্ন সদস্যের প্রতিচ্ছবি ভিন্ন। সুতরাং S এক-এক ফাংশন।
S-1={(-3,-3),(-1,-1),(0,0),(1,1),(3,3)}
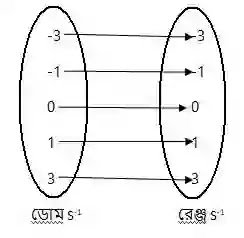
S-1 ফাংশনের ডোমনের ভিন্ন ভিন্ন সদস্যের প্রতিচ্ছবি ভিন্ন। সুতরাং S-1 এক-এক ফাংশন।
(ঙ)
(i) S={(2,1),(2,2),(2,3)}
ডোম S={2}
রেঞ্জ S={1,2,3}
S-1={(1,2),(2,2),(3,2)}
(ii) S এর একই প্রথম উপাদানবিশিষ্ট একাধিক ক্রমজোড় আছে, যেমনঃ (2,1) ও (2,2)। সুতরাং S ফাংশন নয়।
S-1 এর একই প্রথম উপাদান বিশিষ্ট একাধিক ক্রমজোড় নেই। সুতরাং S-1 ফাংশন।
(iii) S ফাংশন নয় তাই এক-এক নয়।
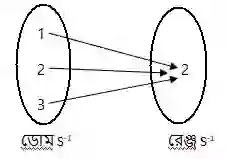
S-1 ফাংশনটির একই দ্বিতীয় উপদান বিশিষ্ট একাধিক ক্রমজোড় রয়েছে। যেমনঃ (1,2), (2,2), (3,2)।
সুতরাং ফাংশনটি S-1 এক-এক নয়।
৯. F(x)=√(x-1) দ্বারা বর্ণিত ফাংশনের জন্য
ক) F(1), F(5) এবং F(10) নির্ণয় কর।
খ) F(a2+1) নির্ণয় কর যেখানে a∈R
গ) F(x)=5 হলে, x নির্ণয় কর।
ঘ) F(x)=y হলে, x নির্ণয় কর যেখানে y≥0।
সমাধানঃ
(ক) দেওয়া আছে, F(x)=√(x-1)
∴ F(1)=√(1-1)=√0=0
F(5)=√(5-1)=√4=2
F(10)=√(10-1)=√9=3
(খ) দেওয়া আছে, F(x)=√(x-1)
F(a2+1)= √(a2+1-1)= √a2=।a।
(গ) দেওয়া আছে, F(x)=√(x-1) এবং F(x)=5
∴ √(x-1)=5
বা, x-1=25 [বর্গ করে]
বা, x=25+1
বা, x=26
(ঘ) দেওয়া আছে, F(x)=√(x-1) এবং F(x)=y
∴ √(x-1)=y
বা, x-1=y2 [বর্গ করে]
বা, x=1+y2
১০. F : R -R, F(x)=x3 ফাংশনের জন্য
ক) ডোম F এবং রেঞ্জ F নির্ণয় কর।
খ) দেখাও যে, F এক-এক ফাংশন।
গ) F-1 নির্ণয় কর।
ঘ) দেখাও যে, F-1 একটি ফাংশন।
সমাধানঃ
ক) দেওয়া আছে, F : R -R, F(x)=x3
x এর যে সকল বাস্তব মানের জন্য F(x) এর বাস্তব মান পাওয়া যাবে সেগুলো F(x) এর ডোমেন হবে।
∴ ডোম F=R
আবার, x এর বাস্তব মানের জন্য y বা x3 ও বাস্তব হবে।
সুতরাং রেঞ্জ F=R.
খ) দেওয়া আছে, F : R -R, F(x)=x3
ধরি, x1, x2 ∈ ডোম F
∴ F(x1)=F(x2)
বা, x13=x23
বা, x1=x2
সুতরাং, F এক-এক ফাংশন (দেখানো হলো)
গ) দেওয়া আছে, F : R -R, F(x)=x3
ধরি, F(x)=y
বা, x=F-1(y)
এখন, y=x3
বা, x3=y
বা, x=y1/3
∴ F-1(y)=y1/3
বা, F-1(x)=x1/3
ঘ) গ হতে পাই, F-1(x)=x1/3
এখানে, F-1(x) এর ডোম =R এবং x এর সকল বাস্তক মানের জন্য F-1(x)=x1/3 এর একটি অনন্য মান পাওয়া যাবে।
∴ F-1(x) একটি ফাংশন (দেখানো হলো)
১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক।
খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক।
সমাধানঃ
(ক) দেওয়া আছে, f(x)=ax+b
ধরি, x1, x2 ∈ ডোম f
এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়।
এখন, f(x1)=ax1+b এবং f(x2)=ax2+b
∴ f(x1)=f(x2)
বা, ax1+b= ax2+b
বা, ax1=ax2
বা, x1=x2
অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন।
এখন ধরি, y=f(x)=ax+b
বা, y=ax+b
বা, ax=y-b
y-b
বা, x=————
a
এখন, f(x)=ax+b
y-b y-b
∴ f(——–)=a.———+b
a a
=y-b+b
=y
=f(x)
অতএব, ফাংশটি অনটু বা সার্বিক।
(খ) দেওয়া আছে, f(x)= √(1-x2)
তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2)
যদি f(a)=f(b) হয়, তবে
√(1-a2)= √(1-b2)
বা, 1-a2=1-b2
বা, -a2=-b2
বা, a2=b2
বা, a=b
অতএব, ফাংশনটি এক-এক ফাংশন।
আবার ধরি, y=f(x)=√(1-x2)
বা, y2=1-x2
বা, x2=1-y2
বা, x=√(1-y2)
এখন, f(x)=√(1-x2)
f(√{1-y2})=√[1-{√(1-y2)}2]
=√{1-(1-y2)}
=√(1-1+y2)
=√y2
=y
=f(x)
∴ ফাংশনটি সার্বিক বা অনটু।
১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1।
সমাধানঃ
দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3
ধরি, y=f(x)=x3+5
বা, y=x3+5 এবং y=f(x)
বা, x3=y-5 বা, x=f-1(y)…….(i)
বা, x=(y-5)1/3……(ii)
(i) ও (ii) হতে,
f-1(y)=(y-5)1/3
বা, f-1(x)=(x-5)1/3
বা, f-1(x)=g(x) [দেওয়া তথ্য হতে]
বা, g=f-1 (দেখানো হলো)
খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর।
সমাধানঃ
দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4
ধরি, a=f(x)=5x-4
বা, a=5x-4 অথবা, a=f(x)
বা, 5x=a+4 বা, x=f-1(a)…..(i)
a+4
বা, x=———- …..(ii)
5
(i) ও (ii) হতে পাই,
a+4
f-1(a)= ————-
5
x+4
বা, f-1(x)=————-
5
x+4
∴ y=f-1(x)=———
5
১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর।
ক) S={(x,y) : 2x-y+5=0}
সমাধানঃ
S-এর বর্ণনাকারী সমীকরণ,
2x-y+5=0
বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো-
x 0 1 -1
y 5 7 3
∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S
এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি।
![১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। সমাধানঃ (ক) দেওয়া আছে, f(x)=ax+b ধরি, x1, x2 ∈ ডোম f এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়। এখন, f(x1)=ax1+b এবং f(x2)=ax2+b ∴ f(x1)=f(x2) বা, ax1+b= ax2+b বা, ax1=ax2 বা, x1=x2 অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন। এখন ধরি, y=f(x)=ax+b বা, y=ax+b বা, ax=y-b y-b বা, x=------------ a এখন, f(x)=ax+b y-b y-b ∴ f(--------)=a.---------+b a a =y-b+b =y =f(x) অতএব, ফাংশটি অনটু বা সার্বিক। (খ) দেওয়া আছে, f(x)= √(1-x2) তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2) যদি f(a)=f(b) হয়, তবে √(1-a2)= √(1-b2) বা, 1-a2=1-b2 বা, -a2=-b2 বা, a2=b2 বা, a=b অতএব, ফাংশনটি এক-এক ফাংশন। আবার ধরি, y=f(x)=√(1-x2) বা, y2=1-x2 বা, x2=1-y2 বা, x=√(1-y2) এখন, f(x)=√(1-x2) f(√{1-y2})=√[1-{√(1-y2)}2] =√{1-(1-y2)} =√(1-1+y2) =√y2 =y =f(x) ∴ ফাংশনটি সার্বিক বা অনটু। ১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3 ধরি, y=f(x)=x3+5 বা, y=x3+5 এবং y=f(x) বা, x3=y-5 বা, x=f-1(y)…….(i) বা, x=(y-5)1/3……(ii) (i) ও (ii) হতে, f-1(y)=(y-5)1/3 বা, f-1(x)=(x-5)1/3 বা, f-1(x)=g(x) [দেওয়া তথ্য হতে] বা, g=f-1 (দেখানো হলো) খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর। সমাধানঃ দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4 ধরি, a=f(x)=5x-4 বা, a=5x-4 অথবা, a=f(x) বা, 5x=a+4 বা, x=f-1(a)…..(i) a+4 বা, x=---------- …..(ii) 5 (i) ও (ii) হতে পাই, a+4 f-1(a)= ------------- 5 x+4 বা, f-1(x)=------------- 5 x+4 ∴ y=f-1(x)=--------- 5 ১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : 2x-y+5=0} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 2x-y+5=0 বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -1 y 5 7 3 ∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। খ) S={(x,y) : x+y=1} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x+y=1 বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -2 y 1 0 3 ∴ L={(0,1),(1,0),(-2,3)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। গ) S={(x,y) : 3x+y=4} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 3x+y=4 বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 2 y 4 1 -2 ∴ L={(0,4),(1,1),(2,-2)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। ঘ) S={(x,y) : x=-2} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত। লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়। ১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : x2+y2=25} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=25 বা, (x-0)2+(y-0)2=52 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়। খ) S={(x,y) : x2+y=9} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=9 বা, (x-0)2+(y-0)2=32 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়। ১৫. দেওয়া আছে, F(x)=2x-1 ক) F(x+1) এবং F(½) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, F(x)=2x-1 F(x+1)=2(x+1)-1 =2x+2-1 =2x+1 F(½)=2.(½)-1 =1-1 =0 খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R। সমাধানঃ দেওয়া আছে, F(x)=2x-1 ∴ F(a)=2a-1 এবং F(b)=2b-1 এখন, F(a)=F(b) এর জন্য 2a-1=2b-1 বা, 2a=2b বা, a=b সুতরাং ফাংশনটি এক-এক। গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর। সমাধানঃ F(x)=y বা, F(x)=2x-1=y [y=2x-1] বা, 2x=y+1 বা, x=½(y+1) এখন, y=1 হলে, ½(1+1)= ½✕2=1 y=3 হলে, ½(3+1)= ½✕4=2 y=5 হলে, ½(5+1)= ½✕6=3 ∴ x এর তিনটি মান 1,2,3 এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5) এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ ১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত। ক) g-1(-3) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, x-3 g(x)=------------- 3 ধরি, y=g(x) x-3 বা, y=------------- 3 বা, 3y=x-3 বা, x=3y+3……..(i) আবার, y=g(x) বা, x=g-1(y)…….(ii) (i) ও (ii) হতে পাই, g-1(y)=3y+3 বা, g-1(-3)=3.(-3)+3 =-9+3 =-6 খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f : RR এবং f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=------------- 3 এখন, f(x)=3x+3 y-3 y-3 ∴ f (----------)=3.-----------+3 3 3 =y-3+3 =y =f(x) ∴ ফাংশনটি সার্বিক। গ) দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=--------- ….(i) 3 এখন, y=f(x) বা, x=f-1(y)……(ii) (i) ও (ii) হতে পাই, y-3 f-1(y)=------------ 3 x-3 বা, f-1(x)=----------....(iii) 3 আবার, দেওয়া আছে, x-3 g(x)=-------------……(iv) 3 (iii) ও (iv) হতে পাই, f-1(x)=g(x) বা, g=f-1 (দেখানো হলো) ১৭. দেওয়া আছে, f(x)= √(x-4) ক) f(x) এর ডোমেন নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)= √(x-4) x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ। f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি x-4≥0 হয় বা, x≥4 হয়। সুতরাং ডোম f={x∈R : x≥4} খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ∴ f(a)= √(a-4) এবং f(b)= √(b-4) এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়। এখন, f(a)=f(b) হলে, √(a-4)= √(b-4) বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে] বা, a=b ∴ ফাংশনটি এক-এক। গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ধরি, y=f(x) বা, x=f-1(y)…….(i) এবং y=f(x)=√(x-4) বা, y=√(x-4) বা, y2=x-4 বা, x-4=y2 বা, x=y2+4……(ii) (i) ও (ii) হতে পাই, f-1(y)=y2+4 বা, f-1(x)=x2+4 x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি। x -1 0 1 f-1(x) 5 4 5 L={(-1,5),(0,4),(1,5)} এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।](http://elessonbd.com/wp-content/uploads/2022/10/13-ka.jpg)
লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।
খ) S={(x,y) : x+y=1}
সমাধানঃ
S-এর বর্ণনাকারী সমীকরণ,
x+y=1
বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো-
x 0 1 -2
y 1 0 3
∴ L={(0,1),(1,0),(-2,3)} ⊂S
এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি।
![১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। সমাধানঃ (ক) দেওয়া আছে, f(x)=ax+b ধরি, x1, x2 ∈ ডোম f এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়। এখন, f(x1)=ax1+b এবং f(x2)=ax2+b ∴ f(x1)=f(x2) বা, ax1+b= ax2+b বা, ax1=ax2 বা, x1=x2 অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন। এখন ধরি, y=f(x)=ax+b বা, y=ax+b বা, ax=y-b y-b বা, x=------------ a এখন, f(x)=ax+b y-b y-b ∴ f(--------)=a.---------+b a a =y-b+b =y =f(x) অতএব, ফাংশটি অনটু বা সার্বিক। (খ) দেওয়া আছে, f(x)= √(1-x2) তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2) যদি f(a)=f(b) হয়, তবে √(1-a2)= √(1-b2) বা, 1-a2=1-b2 বা, -a2=-b2 বা, a2=b2 বা, a=b অতএব, ফাংশনটি এক-এক ফাংশন। আবার ধরি, y=f(x)=√(1-x2) বা, y2=1-x2 বা, x2=1-y2 বা, x=√(1-y2) এখন, f(x)=√(1-x2) f(√{1-y2})=√[1-{√(1-y2)}2] =√{1-(1-y2)} =√(1-1+y2) =√y2 =y =f(x) ∴ ফাংশনটি সার্বিক বা অনটু। ১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3 ধরি, y=f(x)=x3+5 বা, y=x3+5 এবং y=f(x) বা, x3=y-5 বা, x=f-1(y)…….(i) বা, x=(y-5)1/3……(ii) (i) ও (ii) হতে, f-1(y)=(y-5)1/3 বা, f-1(x)=(x-5)1/3 বা, f-1(x)=g(x) [দেওয়া তথ্য হতে] বা, g=f-1 (দেখানো হলো) খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর। সমাধানঃ দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4 ধরি, a=f(x)=5x-4 বা, a=5x-4 অথবা, a=f(x) বা, 5x=a+4 বা, x=f-1(a)…..(i) a+4 বা, x=---------- …..(ii) 5 (i) ও (ii) হতে পাই, a+4 f-1(a)= ------------- 5 x+4 বা, f-1(x)=------------- 5 x+4 ∴ y=f-1(x)=--------- 5 ১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : 2x-y+5=0} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 2x-y+5=0 বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -1 y 5 7 3 ∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। খ) S={(x,y) : x+y=1} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x+y=1 বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -2 y 1 0 3 ∴ L={(0,1),(1,0),(-2,3)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। গ) S={(x,y) : 3x+y=4} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 3x+y=4 বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 2 y 4 1 -2 ∴ L={(0,4),(1,1),(2,-2)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। ঘ) S={(x,y) : x=-2} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত। লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়। ১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : x2+y2=25} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=25 বা, (x-0)2+(y-0)2=52 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়। খ) S={(x,y) : x2+y=9} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=9 বা, (x-0)2+(y-0)2=32 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়। ১৫. দেওয়া আছে, F(x)=2x-1 ক) F(x+1) এবং F(½) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, F(x)=2x-1 F(x+1)=2(x+1)-1 =2x+2-1 =2x+1 F(½)=2.(½)-1 =1-1 =0 খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R। সমাধানঃ দেওয়া আছে, F(x)=2x-1 ∴ F(a)=2a-1 এবং F(b)=2b-1 এখন, F(a)=F(b) এর জন্য 2a-1=2b-1 বা, 2a=2b বা, a=b সুতরাং ফাংশনটি এক-এক। গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর। সমাধানঃ F(x)=y বা, F(x)=2x-1=y [y=2x-1] বা, 2x=y+1 বা, x=½(y+1) এখন, y=1 হলে, ½(1+1)= ½✕2=1 y=3 হলে, ½(3+1)= ½✕4=2 y=5 হলে, ½(5+1)= ½✕6=3 ∴ x এর তিনটি মান 1,2,3 এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5) এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ ১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত। ক) g-1(-3) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, x-3 g(x)=------------- 3 ধরি, y=g(x) x-3 বা, y=------------- 3 বা, 3y=x-3 বা, x=3y+3……..(i) আবার, y=g(x) বা, x=g-1(y)…….(ii) (i) ও (ii) হতে পাই, g-1(y)=3y+3 বা, g-1(-3)=3.(-3)+3 =-9+3 =-6 খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f : RR এবং f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=------------- 3 এখন, f(x)=3x+3 y-3 y-3 ∴ f (----------)=3.-----------+3 3 3 =y-3+3 =y =f(x) ∴ ফাংশনটি সার্বিক। গ) দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=--------- ….(i) 3 এখন, y=f(x) বা, x=f-1(y)……(ii) (i) ও (ii) হতে পাই, y-3 f-1(y)=------------ 3 x-3 বা, f-1(x)=----------....(iii) 3 আবার, দেওয়া আছে, x-3 g(x)=-------------……(iv) 3 (iii) ও (iv) হতে পাই, f-1(x)=g(x) বা, g=f-1 (দেখানো হলো) ১৭. দেওয়া আছে, f(x)= √(x-4) ক) f(x) এর ডোমেন নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)= √(x-4) x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ। f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি x-4≥0 হয় বা, x≥4 হয়। সুতরাং ডোম f={x∈R : x≥4} খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ∴ f(a)= √(a-4) এবং f(b)= √(b-4) এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়। এখন, f(a)=f(b) হলে, √(a-4)= √(b-4) বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে] বা, a=b ∴ ফাংশনটি এক-এক। গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ধরি, y=f(x) বা, x=f-1(y)…….(i) এবং y=f(x)=√(x-4) বা, y=√(x-4) বা, y2=x-4 বা, x-4=y2 বা, x=y2+4……(ii) (i) ও (ii) হতে পাই, f-1(y)=y2+4 বা, f-1(x)=x2+4 x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি। x -1 0 1 f-1(x) 5 4 5 L={(-1,5),(0,4),(1,5)} এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।](http://elessonbd.com/wp-content/uploads/2022/10/13-kha.jpg)
লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।
গ) S={(x,y) : 3x+y=4}
সমাধানঃ
S-এর বর্ণনাকারী সমীকরণ,
3x+y=4
বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো-
x 0 1 2
y 4 1 -2
∴ L={(0,4),(1,1),(2,-2)} ⊂S
এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি।
![১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। সমাধানঃ (ক) দেওয়া আছে, f(x)=ax+b ধরি, x1, x2 ∈ ডোম f এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়। এখন, f(x1)=ax1+b এবং f(x2)=ax2+b ∴ f(x1)=f(x2) বা, ax1+b= ax2+b বা, ax1=ax2 বা, x1=x2 অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন। এখন ধরি, y=f(x)=ax+b বা, y=ax+b বা, ax=y-b y-b বা, x=------------ a এখন, f(x)=ax+b y-b y-b ∴ f(--------)=a.---------+b a a =y-b+b =y =f(x) অতএব, ফাংশটি অনটু বা সার্বিক। (খ) দেওয়া আছে, f(x)= √(1-x2) তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2) যদি f(a)=f(b) হয়, তবে √(1-a2)= √(1-b2) বা, 1-a2=1-b2 বা, -a2=-b2 বা, a2=b2 বা, a=b অতএব, ফাংশনটি এক-এক ফাংশন। আবার ধরি, y=f(x)=√(1-x2) বা, y2=1-x2 বা, x2=1-y2 বা, x=√(1-y2) এখন, f(x)=√(1-x2) f(√{1-y2})=√[1-{√(1-y2)}2] =√{1-(1-y2)} =√(1-1+y2) =√y2 =y =f(x) ∴ ফাংশনটি সার্বিক বা অনটু। ১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3 ধরি, y=f(x)=x3+5 বা, y=x3+5 এবং y=f(x) বা, x3=y-5 বা, x=f-1(y)…….(i) বা, x=(y-5)1/3……(ii) (i) ও (ii) হতে, f-1(y)=(y-5)1/3 বা, f-1(x)=(x-5)1/3 বা, f-1(x)=g(x) [দেওয়া তথ্য হতে] বা, g=f-1 (দেখানো হলো) খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর। সমাধানঃ দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4 ধরি, a=f(x)=5x-4 বা, a=5x-4 অথবা, a=f(x) বা, 5x=a+4 বা, x=f-1(a)…..(i) a+4 বা, x=---------- …..(ii) 5 (i) ও (ii) হতে পাই, a+4 f-1(a)= ------------- 5 x+4 বা, f-1(x)=------------- 5 x+4 ∴ y=f-1(x)=--------- 5 ১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : 2x-y+5=0} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 2x-y+5=0 বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -1 y 5 7 3 ∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। খ) S={(x,y) : x+y=1} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x+y=1 বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -2 y 1 0 3 ∴ L={(0,1),(1,0),(-2,3)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। গ) S={(x,y) : 3x+y=4} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 3x+y=4 বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 2 y 4 1 -2 ∴ L={(0,4),(1,1),(2,-2)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। ঘ) S={(x,y) : x=-2} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত। লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়। ১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : x2+y2=25} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=25 বা, (x-0)2+(y-0)2=52 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়। খ) S={(x,y) : x2+y=9} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=9 বা, (x-0)2+(y-0)2=32 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়। ১৫. দেওয়া আছে, F(x)=2x-1 ক) F(x+1) এবং F(½) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, F(x)=2x-1 F(x+1)=2(x+1)-1 =2x+2-1 =2x+1 F(½)=2.(½)-1 =1-1 =0 খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R। সমাধানঃ দেওয়া আছে, F(x)=2x-1 ∴ F(a)=2a-1 এবং F(b)=2b-1 এখন, F(a)=F(b) এর জন্য 2a-1=2b-1 বা, 2a=2b বা, a=b সুতরাং ফাংশনটি এক-এক। গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর। সমাধানঃ F(x)=y বা, F(x)=2x-1=y [y=2x-1] বা, 2x=y+1 বা, x=½(y+1) এখন, y=1 হলে, ½(1+1)= ½✕2=1 y=3 হলে, ½(3+1)= ½✕4=2 y=5 হলে, ½(5+1)= ½✕6=3 ∴ x এর তিনটি মান 1,2,3 এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5) এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ ১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত। ক) g-1(-3) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, x-3 g(x)=------------- 3 ধরি, y=g(x) x-3 বা, y=------------- 3 বা, 3y=x-3 বা, x=3y+3……..(i) আবার, y=g(x) বা, x=g-1(y)…….(ii) (i) ও (ii) হতে পাই, g-1(y)=3y+3 বা, g-1(-3)=3.(-3)+3 =-9+3 =-6 খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f : RR এবং f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=------------- 3 এখন, f(x)=3x+3 y-3 y-3 ∴ f (----------)=3.-----------+3 3 3 =y-3+3 =y =f(x) ∴ ফাংশনটি সার্বিক। গ) দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=--------- ….(i) 3 এখন, y=f(x) বা, x=f-1(y)……(ii) (i) ও (ii) হতে পাই, y-3 f-1(y)=------------ 3 x-3 বা, f-1(x)=----------....(iii) 3 আবার, দেওয়া আছে, x-3 g(x)=-------------……(iv) 3 (iii) ও (iv) হতে পাই, f-1(x)=g(x) বা, g=f-1 (দেখানো হলো) ১৭. দেওয়া আছে, f(x)= √(x-4) ক) f(x) এর ডোমেন নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)= √(x-4) x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ। f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি x-4≥0 হয় বা, x≥4 হয়। সুতরাং ডোম f={x∈R : x≥4} খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ∴ f(a)= √(a-4) এবং f(b)= √(b-4) এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়। এখন, f(a)=f(b) হলে, √(a-4)= √(b-4) বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে] বা, a=b ∴ ফাংশনটি এক-এক। গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ধরি, y=f(x) বা, x=f-1(y)…….(i) এবং y=f(x)=√(x-4) বা, y=√(x-4) বা, y2=x-4 বা, x-4=y2 বা, x=y2+4……(ii) (i) ও (ii) হতে পাই, f-1(y)=y2+4 বা, f-1(x)=x2+4 x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি। x -1 0 1 f-1(x) 5 4 5 L={(-1,5),(0,4),(1,5)} এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।](http://elessonbd.com/wp-content/uploads/2022/10/13-ga.jpg)
লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।
ঘ) S={(x,y) : x=-2}
সমাধানঃ
S-এর বর্ণনাকারী সমীকরণ,
x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত।
![১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। সমাধানঃ (ক) দেওয়া আছে, f(x)=ax+b ধরি, x1, x2 ∈ ডোম f এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়। এখন, f(x1)=ax1+b এবং f(x2)=ax2+b ∴ f(x1)=f(x2) বা, ax1+b= ax2+b বা, ax1=ax2 বা, x1=x2 অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন। এখন ধরি, y=f(x)=ax+b বা, y=ax+b বা, ax=y-b y-b বা, x=------------ a এখন, f(x)=ax+b y-b y-b ∴ f(--------)=a.---------+b a a =y-b+b =y =f(x) অতএব, ফাংশটি অনটু বা সার্বিক। (খ) দেওয়া আছে, f(x)= √(1-x2) তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2) যদি f(a)=f(b) হয়, তবে √(1-a2)= √(1-b2) বা, 1-a2=1-b2 বা, -a2=-b2 বা, a2=b2 বা, a=b অতএব, ফাংশনটি এক-এক ফাংশন। আবার ধরি, y=f(x)=√(1-x2) বা, y2=1-x2 বা, x2=1-y2 বা, x=√(1-y2) এখন, f(x)=√(1-x2) f(√{1-y2})=√[1-{√(1-y2)}2] =√{1-(1-y2)} =√(1-1+y2) =√y2 =y =f(x) ∴ ফাংশনটি সার্বিক বা অনটু। ১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3 ধরি, y=f(x)=x3+5 বা, y=x3+5 এবং y=f(x) বা, x3=y-5 বা, x=f-1(y)…….(i) বা, x=(y-5)1/3……(ii) (i) ও (ii) হতে, f-1(y)=(y-5)1/3 বা, f-1(x)=(x-5)1/3 বা, f-1(x)=g(x) [দেওয়া তথ্য হতে] বা, g=f-1 (দেখানো হলো) খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর। সমাধানঃ দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4 ধরি, a=f(x)=5x-4 বা, a=5x-4 অথবা, a=f(x) বা, 5x=a+4 বা, x=f-1(a)…..(i) a+4 বা, x=---------- …..(ii) 5 (i) ও (ii) হতে পাই, a+4 f-1(a)= ------------- 5 x+4 বা, f-1(x)=------------- 5 x+4 ∴ y=f-1(x)=--------- 5 ১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : 2x-y+5=0} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 2x-y+5=0 বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -1 y 5 7 3 ∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। খ) S={(x,y) : x+y=1} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x+y=1 বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -2 y 1 0 3 ∴ L={(0,1),(1,0),(-2,3)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। গ) S={(x,y) : 3x+y=4} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 3x+y=4 বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 2 y 4 1 -2 ∴ L={(0,4),(1,1),(2,-2)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। ঘ) S={(x,y) : x=-2} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত। লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়। ১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : x2+y2=25} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=25 বা, (x-0)2+(y-0)2=52 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়। খ) S={(x,y) : x2+y=9} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=9 বা, (x-0)2+(y-0)2=32 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়। ১৫. দেওয়া আছে, F(x)=2x-1 ক) F(x+1) এবং F(½) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, F(x)=2x-1 F(x+1)=2(x+1)-1 =2x+2-1 =2x+1 F(½)=2.(½)-1 =1-1 =0 খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R। সমাধানঃ দেওয়া আছে, F(x)=2x-1 ∴ F(a)=2a-1 এবং F(b)=2b-1 এখন, F(a)=F(b) এর জন্য 2a-1=2b-1 বা, 2a=2b বা, a=b সুতরাং ফাংশনটি এক-এক। গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর। সমাধানঃ F(x)=y বা, F(x)=2x-1=y [y=2x-1] বা, 2x=y+1 বা, x=½(y+1) এখন, y=1 হলে, ½(1+1)= ½✕2=1 y=3 হলে, ½(3+1)= ½✕4=2 y=5 হলে, ½(5+1)= ½✕6=3 ∴ x এর তিনটি মান 1,2,3 এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5) এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ ১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত। ক) g-1(-3) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, x-3 g(x)=------------- 3 ধরি, y=g(x) x-3 বা, y=------------- 3 বা, 3y=x-3 বা, x=3y+3……..(i) আবার, y=g(x) বা, x=g-1(y)…….(ii) (i) ও (ii) হতে পাই, g-1(y)=3y+3 বা, g-1(-3)=3.(-3)+3 =-9+3 =-6 খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f : RR এবং f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=------------- 3 এখন, f(x)=3x+3 y-3 y-3 ∴ f (----------)=3.-----------+3 3 3 =y-3+3 =y =f(x) ∴ ফাংশনটি সার্বিক। গ) দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=--------- ….(i) 3 এখন, y=f(x) বা, x=f-1(y)……(ii) (i) ও (ii) হতে পাই, y-3 f-1(y)=------------ 3 x-3 বা, f-1(x)=----------....(iii) 3 আবার, দেওয়া আছে, x-3 g(x)=-------------……(iv) 3 (iii) ও (iv) হতে পাই, f-1(x)=g(x) বা, g=f-1 (দেখানো হলো) ১৭. দেওয়া আছে, f(x)= √(x-4) ক) f(x) এর ডোমেন নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)= √(x-4) x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ। f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি x-4≥0 হয় বা, x≥4 হয়। সুতরাং ডোম f={x∈R : x≥4} খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ∴ f(a)= √(a-4) এবং f(b)= √(b-4) এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়। এখন, f(a)=f(b) হলে, √(a-4)= √(b-4) বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে] বা, a=b ∴ ফাংশনটি এক-এক। গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ধরি, y=f(x) বা, x=f-1(y)…….(i) এবং y=f(x)=√(x-4) বা, y=√(x-4) বা, y2=x-4 বা, x-4=y2 বা, x=y2+4……(ii) (i) ও (ii) হতে পাই, f-1(y)=y2+4 বা, f-1(x)=x2+4 x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি। x -1 0 1 f-1(x) 5 4 5 L={(-1,5),(0,4),(1,5)} এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।](http://elessonbd.com/wp-content/uploads/2022/10/13-gha.jpg)
লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়।
১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর।
ক) S={(x,y) : x2+y2=25}
সমাধানঃ
S-এর বর্ণনাকারী সমীকরণ,
x2+y2=25
বা, (x-0)2+(y-0)2=52
∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো।
![১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। সমাধানঃ (ক) দেওয়া আছে, f(x)=ax+b ধরি, x1, x2 ∈ ডোম f এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়। এখন, f(x1)=ax1+b এবং f(x2)=ax2+b ∴ f(x1)=f(x2) বা, ax1+b= ax2+b বা, ax1=ax2 বা, x1=x2 অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন। এখন ধরি, y=f(x)=ax+b বা, y=ax+b বা, ax=y-b y-b বা, x=------------ a এখন, f(x)=ax+b y-b y-b ∴ f(--------)=a.---------+b a a =y-b+b =y =f(x) অতএব, ফাংশটি অনটু বা সার্বিক। (খ) দেওয়া আছে, f(x)= √(1-x2) তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2) যদি f(a)=f(b) হয়, তবে √(1-a2)= √(1-b2) বা, 1-a2=1-b2 বা, -a2=-b2 বা, a2=b2 বা, a=b অতএব, ফাংশনটি এক-এক ফাংশন। আবার ধরি, y=f(x)=√(1-x2) বা, y2=1-x2 বা, x2=1-y2 বা, x=√(1-y2) এখন, f(x)=√(1-x2) f(√{1-y2})=√[1-{√(1-y2)}2] =√{1-(1-y2)} =√(1-1+y2) =√y2 =y =f(x) ∴ ফাংশনটি সার্বিক বা অনটু। ১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3 ধরি, y=f(x)=x3+5 বা, y=x3+5 এবং y=f(x) বা, x3=y-5 বা, x=f-1(y)…….(i) বা, x=(y-5)1/3……(ii) (i) ও (ii) হতে, f-1(y)=(y-5)1/3 বা, f-1(x)=(x-5)1/3 বা, f-1(x)=g(x) [দেওয়া তথ্য হতে] বা, g=f-1 (দেখানো হলো) খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর। সমাধানঃ দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4 ধরি, a=f(x)=5x-4 বা, a=5x-4 অথবা, a=f(x) বা, 5x=a+4 বা, x=f-1(a)…..(i) a+4 বা, x=---------- …..(ii) 5 (i) ও (ii) হতে পাই, a+4 f-1(a)= ------------- 5 x+4 বা, f-1(x)=------------- 5 x+4 ∴ y=f-1(x)=--------- 5 ১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : 2x-y+5=0} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 2x-y+5=0 বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -1 y 5 7 3 ∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। খ) S={(x,y) : x+y=1} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x+y=1 বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -2 y 1 0 3 ∴ L={(0,1),(1,0),(-2,3)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। গ) S={(x,y) : 3x+y=4} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 3x+y=4 বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 2 y 4 1 -2 ∴ L={(0,4),(1,1),(2,-2)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। ঘ) S={(x,y) : x=-2} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত। লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়। ১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : x2+y2=25} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=25 বা, (x-0)2+(y-0)2=52 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়। খ) S={(x,y) : x2+y=9} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=9 বা, (x-0)2+(y-0)2=32 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়। ১৫. দেওয়া আছে, F(x)=2x-1 ক) F(x+1) এবং F(½) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, F(x)=2x-1 F(x+1)=2(x+1)-1 =2x+2-1 =2x+1 F(½)=2.(½)-1 =1-1 =0 খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R। সমাধানঃ দেওয়া আছে, F(x)=2x-1 ∴ F(a)=2a-1 এবং F(b)=2b-1 এখন, F(a)=F(b) এর জন্য 2a-1=2b-1 বা, 2a=2b বা, a=b সুতরাং ফাংশনটি এক-এক। গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর। সমাধানঃ F(x)=y বা, F(x)=2x-1=y [y=2x-1] বা, 2x=y+1 বা, x=½(y+1) এখন, y=1 হলে, ½(1+1)= ½✕2=1 y=3 হলে, ½(3+1)= ½✕4=2 y=5 হলে, ½(5+1)= ½✕6=3 ∴ x এর তিনটি মান 1,2,3 এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5) এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ ১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত। ক) g-1(-3) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, x-3 g(x)=------------- 3 ধরি, y=g(x) x-3 বা, y=------------- 3 বা, 3y=x-3 বা, x=3y+3……..(i) আবার, y=g(x) বা, x=g-1(y)…….(ii) (i) ও (ii) হতে পাই, g-1(y)=3y+3 বা, g-1(-3)=3.(-3)+3 =-9+3 =-6 খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f : RR এবং f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=------------- 3 এখন, f(x)=3x+3 y-3 y-3 ∴ f (----------)=3.-----------+3 3 3 =y-3+3 =y =f(x) ∴ ফাংশনটি সার্বিক। গ) দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=--------- ….(i) 3 এখন, y=f(x) বা, x=f-1(y)……(ii) (i) ও (ii) হতে পাই, y-3 f-1(y)=------------ 3 x-3 বা, f-1(x)=----------....(iii) 3 আবার, দেওয়া আছে, x-3 g(x)=-------------……(iv) 3 (iii) ও (iv) হতে পাই, f-1(x)=g(x) বা, g=f-1 (দেখানো হলো) ১৭. দেওয়া আছে, f(x)= √(x-4) ক) f(x) এর ডোমেন নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)= √(x-4) x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ। f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি x-4≥0 হয় বা, x≥4 হয়। সুতরাং ডোম f={x∈R : x≥4} খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ∴ f(a)= √(a-4) এবং f(b)= √(b-4) এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়। এখন, f(a)=f(b) হলে, √(a-4)= √(b-4) বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে] বা, a=b ∴ ফাংশনটি এক-এক। গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ধরি, y=f(x) বা, x=f-1(y)…….(i) এবং y=f(x)=√(x-4) বা, y=√(x-4) বা, y2=x-4 বা, x-4=y2 বা, x=y2+4……(ii) (i) ও (ii) হতে পাই, f-1(y)=y2+4 বা, f-1(x)=x2+4 x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি। x -1 0 1 f-1(x) 5 4 5 L={(-1,5),(0,4),(1,5)} এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।](http://elessonbd.com/wp-content/uploads/2022/10/14-ka.jpg)
লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়।
খ) S={(x,y) : x2+y=9}
সমাধানঃ
S-এর বর্ণনাকারী সমীকরণ,
x2+y2=9
বা, (x-0)2+(y-0)2=32
∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো।
![১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। সমাধানঃ (ক) দেওয়া আছে, f(x)=ax+b ধরি, x1, x2 ∈ ডোম f এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়। এখন, f(x1)=ax1+b এবং f(x2)=ax2+b ∴ f(x1)=f(x2) বা, ax1+b= ax2+b বা, ax1=ax2 বা, x1=x2 অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন। এখন ধরি, y=f(x)=ax+b বা, y=ax+b বা, ax=y-b y-b বা, x=------------ a এখন, f(x)=ax+b y-b y-b ∴ f(--------)=a.---------+b a a =y-b+b =y =f(x) অতএব, ফাংশটি অনটু বা সার্বিক। (খ) দেওয়া আছে, f(x)= √(1-x2) তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2) যদি f(a)=f(b) হয়, তবে √(1-a2)= √(1-b2) বা, 1-a2=1-b2 বা, -a2=-b2 বা, a2=b2 বা, a=b অতএব, ফাংশনটি এক-এক ফাংশন। আবার ধরি, y=f(x)=√(1-x2) বা, y2=1-x2 বা, x2=1-y2 বা, x=√(1-y2) এখন, f(x)=√(1-x2) f(√{1-y2})=√[1-{√(1-y2)}2] =√{1-(1-y2)} =√(1-1+y2) =√y2 =y =f(x) ∴ ফাংশনটি সার্বিক বা অনটু। ১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3 ধরি, y=f(x)=x3+5 বা, y=x3+5 এবং y=f(x) বা, x3=y-5 বা, x=f-1(y)…….(i) বা, x=(y-5)1/3……(ii) (i) ও (ii) হতে, f-1(y)=(y-5)1/3 বা, f-1(x)=(x-5)1/3 বা, f-1(x)=g(x) [দেওয়া তথ্য হতে] বা, g=f-1 (দেখানো হলো) খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর। সমাধানঃ দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4 ধরি, a=f(x)=5x-4 বা, a=5x-4 অথবা, a=f(x) বা, 5x=a+4 বা, x=f-1(a)…..(i) a+4 বা, x=---------- …..(ii) 5 (i) ও (ii) হতে পাই, a+4 f-1(a)= ------------- 5 x+4 বা, f-1(x)=------------- 5 x+4 ∴ y=f-1(x)=--------- 5 ১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : 2x-y+5=0} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 2x-y+5=0 বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -1 y 5 7 3 ∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। খ) S={(x,y) : x+y=1} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x+y=1 বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -2 y 1 0 3 ∴ L={(0,1),(1,0),(-2,3)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। গ) S={(x,y) : 3x+y=4} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 3x+y=4 বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 2 y 4 1 -2 ∴ L={(0,4),(1,1),(2,-2)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। ঘ) S={(x,y) : x=-2} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত। লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়। ১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : x2+y2=25} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=25 বা, (x-0)2+(y-0)2=52 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়। খ) S={(x,y) : x2+y=9} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=9 বা, (x-0)2+(y-0)2=32 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়। ১৫. দেওয়া আছে, F(x)=2x-1 ক) F(x+1) এবং F(½) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, F(x)=2x-1 F(x+1)=2(x+1)-1 =2x+2-1 =2x+1 F(½)=2.(½)-1 =1-1 =0 খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R। সমাধানঃ দেওয়া আছে, F(x)=2x-1 ∴ F(a)=2a-1 এবং F(b)=2b-1 এখন, F(a)=F(b) এর জন্য 2a-1=2b-1 বা, 2a=2b বা, a=b সুতরাং ফাংশনটি এক-এক। গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর। সমাধানঃ F(x)=y বা, F(x)=2x-1=y [y=2x-1] বা, 2x=y+1 বা, x=½(y+1) এখন, y=1 হলে, ½(1+1)= ½✕2=1 y=3 হলে, ½(3+1)= ½✕4=2 y=5 হলে, ½(5+1)= ½✕6=3 ∴ x এর তিনটি মান 1,2,3 এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5) এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ ১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত। ক) g-1(-3) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, x-3 g(x)=------------- 3 ধরি, y=g(x) x-3 বা, y=------------- 3 বা, 3y=x-3 বা, x=3y+3……..(i) আবার, y=g(x) বা, x=g-1(y)…….(ii) (i) ও (ii) হতে পাই, g-1(y)=3y+3 বা, g-1(-3)=3.(-3)+3 =-9+3 =-6 খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f : RR এবং f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=------------- 3 এখন, f(x)=3x+3 y-3 y-3 ∴ f (----------)=3.-----------+3 3 3 =y-3+3 =y =f(x) ∴ ফাংশনটি সার্বিক। গ) দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=--------- ….(i) 3 এখন, y=f(x) বা, x=f-1(y)……(ii) (i) ও (ii) হতে পাই, y-3 f-1(y)=------------ 3 x-3 বা, f-1(x)=----------....(iii) 3 আবার, দেওয়া আছে, x-3 g(x)=-------------……(iv) 3 (iii) ও (iv) হতে পাই, f-1(x)=g(x) বা, g=f-1 (দেখানো হলো) ১৭. দেওয়া আছে, f(x)= √(x-4) ক) f(x) এর ডোমেন নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)= √(x-4) x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ। f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি x-4≥0 হয় বা, x≥4 হয়। সুতরাং ডোম f={x∈R : x≥4} খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ∴ f(a)= √(a-4) এবং f(b)= √(b-4) এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়। এখন, f(a)=f(b) হলে, √(a-4)= √(b-4) বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে] বা, a=b ∴ ফাংশনটি এক-এক। গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ধরি, y=f(x) বা, x=f-1(y)…….(i) এবং y=f(x)=√(x-4) বা, y=√(x-4) বা, y2=x-4 বা, x-4=y2 বা, x=y2+4……(ii) (i) ও (ii) হতে পাই, f-1(y)=y2+4 বা, f-1(x)=x2+4 x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি। x -1 0 1 f-1(x) 5 4 5 L={(-1,5),(0,4),(1,5)} এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।](http://elessonbd.com/wp-content/uploads/2022/10/14-kha.jpg)
লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়।
১৫. দেওয়া আছে, F(x)=2x-1
ক) F(x+1) এবং F(½) এর মান নির্ণয় কর।
সমাধানঃ
দেওয়া আছে, F(x)=2x-1
F(x+1)=2(x+1)-1
=2x+2-1
=2x+1
F(½)=2.(½)-1
=1-1
=0
খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R।
সমাধানঃ
দেওয়া আছে, F(x)=2x-1
∴ F(a)=2a-1 এবং F(b)=2b-1
এখন, F(a)=F(b) এর জন্য
2a-1=2b-1
বা, 2a=2b
বা, a=b
সুতরাং ফাংশনটি এক-এক।
গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর।
সমাধানঃ
F(x)=y
বা, F(x)=2x-1=y [y=2x-1]
বা, 2x=y+1
বা, x=½(y+1)
এখন, y=1 হলে, ½(1+1)= ½✕2=1
y=3 হলে, ½(3+1)= ½✕4=2
y=5 হলে, ½(5+1)= ½✕6=3
∴ x এর তিনটি মান 1,2,3
এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5)
এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ
![১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। সমাধানঃ (ক) দেওয়া আছে, f(x)=ax+b ধরি, x1, x2 ∈ ডোম f এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়। এখন, f(x1)=ax1+b এবং f(x2)=ax2+b ∴ f(x1)=f(x2) বা, ax1+b= ax2+b বা, ax1=ax2 বা, x1=x2 অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন। এখন ধরি, y=f(x)=ax+b বা, y=ax+b বা, ax=y-b y-b বা, x=------------ a এখন, f(x)=ax+b y-b y-b ∴ f(--------)=a.---------+b a a =y-b+b =y =f(x) অতএব, ফাংশটি অনটু বা সার্বিক। (খ) দেওয়া আছে, f(x)= √(1-x2) তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2) যদি f(a)=f(b) হয়, তবে √(1-a2)= √(1-b2) বা, 1-a2=1-b2 বা, -a2=-b2 বা, a2=b2 বা, a=b অতএব, ফাংশনটি এক-এক ফাংশন। আবার ধরি, y=f(x)=√(1-x2) বা, y2=1-x2 বা, x2=1-y2 বা, x=√(1-y2) এখন, f(x)=√(1-x2) f(√{1-y2})=√[1-{√(1-y2)}2] =√{1-(1-y2)} =√(1-1+y2) =√y2 =y =f(x) ∴ ফাংশনটি সার্বিক বা অনটু। ১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3 ধরি, y=f(x)=x3+5 বা, y=x3+5 এবং y=f(x) বা, x3=y-5 বা, x=f-1(y)…….(i) বা, x=(y-5)1/3……(ii) (i) ও (ii) হতে, f-1(y)=(y-5)1/3 বা, f-1(x)=(x-5)1/3 বা, f-1(x)=g(x) [দেওয়া তথ্য হতে] বা, g=f-1 (দেখানো হলো) খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর। সমাধানঃ দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4 ধরি, a=f(x)=5x-4 বা, a=5x-4 অথবা, a=f(x) বা, 5x=a+4 বা, x=f-1(a)…..(i) a+4 বা, x=---------- …..(ii) 5 (i) ও (ii) হতে পাই, a+4 f-1(a)= ------------- 5 x+4 বা, f-1(x)=------------- 5 x+4 ∴ y=f-1(x)=--------- 5 ১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : 2x-y+5=0} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 2x-y+5=0 বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -1 y 5 7 3 ∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। খ) S={(x,y) : x+y=1} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x+y=1 বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -2 y 1 0 3 ∴ L={(0,1),(1,0),(-2,3)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। গ) S={(x,y) : 3x+y=4} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 3x+y=4 বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 2 y 4 1 -2 ∴ L={(0,4),(1,1),(2,-2)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। ঘ) S={(x,y) : x=-2} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত। লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়। ১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : x2+y2=25} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=25 বা, (x-0)2+(y-0)2=52 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়। খ) S={(x,y) : x2+y=9} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=9 বা, (x-0)2+(y-0)2=32 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়। ১৫. দেওয়া আছে, F(x)=2x-1 ক) F(x+1) এবং F(½) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, F(x)=2x-1 F(x+1)=2(x+1)-1 =2x+2-1 =2x+1 F(½)=2.(½)-1 =1-1 =0 খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R। সমাধানঃ দেওয়া আছে, F(x)=2x-1 ∴ F(a)=2a-1 এবং F(b)=2b-1 এখন, F(a)=F(b) এর জন্য 2a-1=2b-1 বা, 2a=2b বা, a=b সুতরাং ফাংশনটি এক-এক। গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর। সমাধানঃ F(x)=y বা, F(x)=2x-1=y [y=2x-1] বা, 2x=y+1 বা, x=½(y+1) এখন, y=1 হলে, ½(1+1)= ½✕2=1 y=3 হলে, ½(3+1)= ½✕4=2 y=5 হলে, ½(5+1)= ½✕6=3 ∴ x এর তিনটি মান 1,2,3 এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5) এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ ১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত। ক) g-1(-3) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, x-3 g(x)=------------- 3 ধরি, y=g(x) x-3 বা, y=------------- 3 বা, 3y=x-3 বা, x=3y+3……..(i) আবার, y=g(x) বা, x=g-1(y)…….(ii) (i) ও (ii) হতে পাই, g-1(y)=3y+3 বা, g-1(-3)=3.(-3)+3 =-9+3 =-6 খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f : RR এবং f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=------------- 3 এখন, f(x)=3x+3 y-3 y-3 ∴ f (----------)=3.-----------+3 3 3 =y-3+3 =y =f(x) ∴ ফাংশনটি সার্বিক। গ) দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=--------- ….(i) 3 এখন, y=f(x) বা, x=f-1(y)……(ii) (i) ও (ii) হতে পাই, y-3 f-1(y)=------------ 3 x-3 বা, f-1(x)=----------....(iii) 3 আবার, দেওয়া আছে, x-3 g(x)=-------------……(iv) 3 (iii) ও (iv) হতে পাই, f-1(x)=g(x) বা, g=f-1 (দেখানো হলো) ১৭. দেওয়া আছে, f(x)= √(x-4) ক) f(x) এর ডোমেন নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)= √(x-4) x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ। f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি x-4≥0 হয় বা, x≥4 হয়। সুতরাং ডোম f={x∈R : x≥4} খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ∴ f(a)= √(a-4) এবং f(b)= √(b-4) এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়। এখন, f(a)=f(b) হলে, √(a-4)= √(b-4) বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে] বা, a=b ∴ ফাংশনটি এক-এক। গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ধরি, y=f(x) বা, x=f-1(y)…….(i) এবং y=f(x)=√(x-4) বা, y=√(x-4) বা, y2=x-4 বা, x-4=y2 বা, x=y2+4……(ii) (i) ও (ii) হতে পাই, f-1(y)=y2+4 বা, f-1(x)=x2+4 x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি। x -1 0 1 f-1(x) 5 4 5 L={(-1,5),(0,4),(1,5)} এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।](http://elessonbd.com/wp-content/uploads/2022/10/15-ga.jpg)
১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত।
ক) g-1(-3) এর মান নির্ণয় কর।
সমাধানঃ
দেওয়া আছে,
x-3
g(x)=————-
3
ধরি, y=g(x)
x-3
বা, y=————-
3
বা, 3y=x-3
বা, x=3y+3……..(i)
আবার, y=g(x)
বা, x=g-1(y)…….(ii)
(i) ও (ii) হতে পাই,
g-1(y)=3y+3
বা, g-1(-3)=3.(-3)+3
=-9+3
=-6
খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর।
সমাধানঃ
দেওয়া আছে, f : RR এবং f(x)=3x+3
ধরি, y=f(x)
বা, y=3x+3
বা, 3x=y-3
y-3
বা, x=————-
3
এখন, f(x)=3x+3
y-3 y-3
∴ f (———-)=3.———–+3
3 3
=y-3+3
=y
=f(x)
∴ ফাংশনটি সার্বিক।
গ) দেখাও যে, g=f-1।
সমাধানঃ
দেওয়া আছে, f(x)=3x+3
ধরি, y=f(x)
বা, y=3x+3
বা, 3x=y-3
y-3
বা, x=——— ….(i)
3
এখন,
y=f(x)
বা, x=f-1(y)……(ii)
(i) ও (ii) হতে পাই,
y-3
f-1(y)=————
3
x-3
বা, f-1(x)=———-….(iii)
3
আবার, দেওয়া আছে,
x-3
g(x)=————-……(iv)
3
(iii) ও (iv) হতে পাই,
f-1(x)=g(x)
বা, g=f-1 (দেখানো হলো)
১৭. দেওয়া আছে, f(x)= √(x-4)
ক) f(x) এর ডোমেন নির্ণয় কর।
সমাধানঃ
দেওয়া আছে, f(x)= √(x-4)
x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ।
f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি
x-4≥0 হয়
বা, x≥4 হয়।
সুতরাং ডোম f={x∈R : x≥4}
খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর।
সমাধানঃ
দেওয়া আছে, f(x)=√(x-4)
∴ f(a)= √(a-4) এবং f(b)= √(b-4)
এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়।
এখন, f(a)=f(b) হলে,
√(a-4)= √(b-4)
বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে]
বা, a=b
∴ ফাংশনটি এক-এক।
গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর।
সমাধানঃ
দেওয়া আছে, f(x)=√(x-4)
ধরি, y=f(x)
বা, x=f-1(y)…….(i)
এবং y=f(x)=√(x-4)
বা, y=√(x-4)
বা, y2=x-4
বা, x-4=y2
বা, x=y2+4……(ii)
(i) ও (ii) হতে পাই,
f-1(y)=y2+4
বা, f-1(x)=x2+4
x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি।
x -1 0 1
f-1(x) 5 4 5
L={(-1,5),(0,4),(1,5)}
এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি।
![১১. ক) f : R R একটি ফাংশন যা f(x)=ax+b; a,b ∈ R দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। খ) f : [0,1][0,1]ফাংশনটি f(x)=√(1-x2) দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক। সমাধানঃ (ক) দেওয়া আছে, f(x)=ax+b ধরি, x1, x2 ∈ ডোম f এখন, f(x1)=f(x2) এর জন্য f এক-এক ফাংশন হবে যদি এবং কেবল যদি x1=x2 হয়। এখন, f(x1)=ax1+b এবং f(x2)=ax2+b ∴ f(x1)=f(x2) বা, ax1+b= ax2+b বা, ax1=ax2 বা, x1=x2 অতএব, প্রদত্ত ফাংশন এক-এক ফাংশন। এখন ধরি, y=f(x)=ax+b বা, y=ax+b বা, ax=y-b y-b বা, x=------------ a এখন, f(x)=ax+b y-b y-b ∴ f(--------)=a.---------+b a a =y-b+b =y =f(x) অতএব, ফাংশটি অনটু বা সার্বিক। (খ) দেওয়া আছে, f(x)= √(1-x2) তাহলে, f(a)= √(1-a2) এবং f(b)=√(1-b2) যদি f(a)=f(b) হয়, তবে √(1-a2)= √(1-b2) বা, 1-a2=1-b2 বা, -a2=-b2 বা, a2=b2 বা, a=b অতএব, ফাংশনটি এক-এক ফাংশন। আবার ধরি, y=f(x)=√(1-x2) বা, y2=1-x2 বা, x2=1-y2 বা, x=√(1-y2) এখন, f(x)=√(1-x2) f(√{1-y2})=√[1-{√(1-y2)}2] =√{1-(1-y2)} =√(1-1+y2) =√y2 =y =f(x) ∴ ফাংশনটি সার্বিক বা অনটু। ১২. ক) যদি f : RR এবং g : RR ফাংশনদ্বয় f(x)=x3+5 এবং g(x)=(x-5)1/3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=x3+5 এবং g(x)=(x-5)1/3 ধরি, y=f(x)=x3+5 বা, y=x3+5 এবং y=f(x) বা, x3=y-5 বা, x=f-1(y)…….(i) বা, x=(y-5)1/3……(ii) (i) ও (ii) হতে, f-1(y)=(y-5)1/3 বা, f-1(x)=(x-5)1/3 বা, f-1(x)=g(x) [দেওয়া তথ্য হতে] বা, g=f-1 (দেখানো হলো) খ) যদি f : RR ফাংশনটি f(x)=5x-4 দ্বারা সংজ্ঞায়িত হয়, তবে y=f-1(x) নির্ণয় কর। সমাধানঃ দেওয়া আছে, f : RR ফাংশনটি f(x)=5x-4 ধরি, a=f(x)=5x-4 বা, a=5x-4 অথবা, a=f(x) বা, 5x=a+4 বা, x=f-1(a)…..(i) a+4 বা, x=---------- …..(ii) 5 (i) ও (ii) হতে পাই, a+4 f-1(a)= ------------- 5 x+4 বা, f-1(x)=------------- 5 x+4 ∴ y=f-1(x)=--------- 5 ১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : 2x-y+5=0} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 2x-y+5=0 বা, y=2x+5 থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -1 y 5 7 3 ∴ L={(0,5),(1,7),(-1,3),(2,9),(-2,1)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। খ) S={(x,y) : x+y=1} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x+y=1 বা, y=1-x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 -2 y 1 0 3 ∴ L={(0,1),(1,0),(-2,3)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। গ) S={(x,y) : 3x+y=4} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, 3x+y=4 বা, y=4-3x থেকে x ও y এর কয়েকটি সংশ্লিষ্ট মান নিচের ছকে নির্ণয় করা হলো- x 0 1 2 y 4 1 -2 ∴ L={(0,4),(1,1),(2,-2)} ⊂S এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর S এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন। ঘ) S={(x,y) : x=-2} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x=-2 তে y যুক্ত কোনো প্পদ নেই। y এর মান যাই হোক না কেন x এর মান সর্বদাই -2. S অন্বয়ের লেখচিত্র হলো y অক্ষের সমান্তরাল রেখা যা মূলবিন্দু হতে 2 একক বামে অবস্থিত। লেখচিত্রে, y অক্ষের সমান্তরাল রেখার ওপর অসংখ্য বিন্দু আছে। সুতরাং এটি একটি ফাংশন নয়। ১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর। ক) S={(x,y) : x2+y2=25} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=25 বা, (x-0)2+(y-0)2=52 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 5. ছক কাগজে (0,0) বিন্দু পাতন করে একে 5 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,5) ও (0,-5) অবস্থিত। সুতরাং S একটি ফাংশন নয়। খ) S={(x,y) : x2+y=9} সমাধানঃ S-এর বর্ণনাকারী সমীকরণ, x2+y2=9 বা, (x-0)2+(y-0)2=32 ∴S এর লেখ একটি বৃত্ত যার কেন্দ্র (0,0) এবং ব্যাসার্ধ 3. ছক কাগজে (0,0) বিন্দু পাতন করে একে 3 একক ব্যাসার্ধ নিয়ে একটি বৃত্ত আকলেই S এর লেখ পাওয়া যাবে। নিচে তা দেখানো হলো। লেখচিত্রে দেখা যায় y অক্ষের ওপর দুইটি বিন্দু (0,3) ও (0,-3) অবস্থিত। সুতরাং S একটি ফাংশন নয়। ১৫. দেওয়া আছে, F(x)=2x-1 ক) F(x+1) এবং F(½) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, F(x)=2x-1 F(x+1)=2(x+1)-1 =2x+2-1 =2x+1 F(½)=2.(½)-1 =1-1 =0 খ) F(x) ফাংশনটি এক.এক. কিনা তা যাচাই কর, যখন x,y∈R। সমাধানঃ দেওয়া আছে, F(x)=2x-1 ∴ F(a)=2a-1 এবং F(b)=2b-1 এখন, F(a)=F(b) এর জন্য 2a-1=2b-1 বা, 2a=2b বা, a=b সুতরাং ফাংশনটি এক-এক। গ) F(x)=y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y=2x-1 সমীকরণটির লেখচিত্র অঙ্কন কর। সমাধানঃ F(x)=y বা, F(x)=2x-1=y [y=2x-1] বা, 2x=y+1 বা, x=½(y+1) এখন, y=1 হলে, ½(1+1)= ½✕2=1 y=3 হলে, ½(3+1)= ½✕4=2 y=5 হলে, ½(5+1)= ½✕6=3 ∴ x এর তিনটি মান 1,2,3 এখানে, ক্রমজোড় তিনটি (1,1), (2,3), (3,5) এবং এই তিনটি বিন্দু দ্বারা অঙ্কিত লেখচিত্র নিন্মরূপঃ ১৬. f : RR এবং g : RR ফাংশন দুইটি যথাক্রমে f(x)=3x+3 এবং g(x)=(x-3)/3 দ্বারা সংজ্ঞায়িত। ক) g-1(-3) এর মান নির্ণয় কর। সমাধানঃ দেওয়া আছে, x-3 g(x)=------------- 3 ধরি, y=g(x) x-3 বা, y=------------- 3 বা, 3y=x-3 বা, x=3y+3……..(i) আবার, y=g(x) বা, x=g-1(y)…….(ii) (i) ও (ii) হতে পাই, g-1(y)=3y+3 বা, g-1(-3)=3.(-3)+3 =-9+3 =-6 খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f : RR এবং f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=------------- 3 এখন, f(x)=3x+3 y-3 y-3 ∴ f (----------)=3.-----------+3 3 3 =y-3+3 =y =f(x) ∴ ফাংশনটি সার্বিক। গ) দেখাও যে, g=f-1। সমাধানঃ দেওয়া আছে, f(x)=3x+3 ধরি, y=f(x) বা, y=3x+3 বা, 3x=y-3 y-3 বা, x=--------- ….(i) 3 এখন, y=f(x) বা, x=f-1(y)……(ii) (i) ও (ii) হতে পাই, y-3 f-1(y)=------------ 3 x-3 বা, f-1(x)=----------....(iii) 3 আবার, দেওয়া আছে, x-3 g(x)=-------------……(iv) 3 (iii) ও (iv) হতে পাই, f-1(x)=g(x) বা, g=f-1 (দেখানো হলো) ১৭. দেওয়া আছে, f(x)= √(x-4) ক) f(x) এর ডোমেন নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)= √(x-4) x এর মান ডোমেন হলে f(x) এর মান হবে রেঞ্জ। f(x) এর বাস্তব মান পাওয়া যাবে যদি এবং কেবল যদি x-4≥0 হয় বা, x≥4 হয়। সুতরাং ডোম f={x∈R : x≥4} খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ∴ f(a)= √(a-4) এবং f(b)= √(b-4) এখন, f(a)=f(b) এর জন্য ফাংশনটি এক-এক হবে যদি এবং কেবল যদি a=b হয়। এখন, f(a)=f(b) হলে, √(a-4)= √(b-4) বা, a-4=b-4 [উভয়পক্ষকে বর্গ করে] বা, a=b ∴ ফাংশনটি এক-এক। গ) f-1(x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর। সমাধানঃ দেওয়া আছে, f(x)=√(x-4) ধরি, y=f(x) বা, x=f-1(y)…….(i) এবং y=f(x)=√(x-4) বা, y=√(x-4) বা, y2=x-4 বা, x-4=y2 বা, x=y2+4……(ii) (i) ও (ii) হতে পাই, f-1(y)=y2+4 বা, f-1(x)=x2+4 x এর কয়েকটি মানের জন্য f-1(x) এর মান নির্ণয় করি। x -1 0 1 f-1(x) 5 4 5 L={(-1,5),(0,4),(1,5)} এখন, উপরোক্ত বিন্দুগুলো নিয়ে নিচের লেখচিত্র আঁকি। লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।](http://elessonbd.com/wp-content/uploads/2022/10/17-ga.jpg)
লেখচিত্রে, y অক্ষের সমান্তরাল কোনো রেখার ওপর f-1(x) এর দুইটি বিন্দু নেই। সুতরাং এটি একটি ফাংশন।

